ProgrammingAlgorithm

빅 오 분석법(Big-O Analysis)으로 알고리즘 성능시간 분석하기

🗓 ⏰ 소요시간 12 분

알고리즘을 풀거나 프로그래밍 면접을 할 때 빅 오 분석법 (Big-O Analysis) 은 유용합니다. 빅 오 분석법은 입력 값의 개수에 따라서 알고리즘의 성능을 분석하는 방법입니다. 이 방법을 통해서 간단하게 알고리즘의 성능을 따져볼 수 있습니다.

주어진 배열 내에서 최대값을 찾는 두 알고리즘을 예로 들어보겠습니다. 첫번째 알고리즘 compareToMax 는 최대값을 하나 정해놓고 다른 값들과 최대값을 비교해나가는 알고리즘입니다.

compareToMax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

int compareToMax(int[] arr) {

    int n = arr.length;
    int max = 0;

    // 배열에 원소없는 경우 -1 리턴
    if (n <= 0) {
        return -1;
    }

    // 배열 첫번째 값을 최대값으로 설정
    max = arr[0];

    // 모든 값을 최대값과 비교
    for (int i = 0; i < n; i++) {
        if (arr[i] > max) {
            max = arr[i];
        }
    }

    return max;
}

두번째 알고리즘 compareToAll 은 최대값 하나와 비교하는 것이 아니라 배열 내 각 원소들과 비교해서 최대값 여부를 판단하는 알고리즘입니다.

compareToAll
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
static int compareToAll(int[] arr) {

    int n = arr.length;

    if (n <= 0) {
        return -1;
    }

    int i, j;

    boolean isMax;
    for (i = n - 1; i > 0; i--) {
        isMax = true;
        for (j = 0; j < n; j++) {
            if (arr[j] > arr[i]) {
                isMax = false;
            }
        }
        if (isMax) {
            break;
        }
    }

    return arr[i];
}

두 알고리즘 모두 정상적으로 최대값을 찾아주는 알고리즘입니다. 이 두가지 알고리즘을 가지고 성능을 비교해보겠습니다.

빅 오 분석법의 원리

빅 오 분석법에서는 입력 값의 크기(개수)를 n개라고 가정합니다. 이 알고리즘에서는 배열에 있는 원소의 개수가 n이 될 것입니다. 이 입력에 대해 어떤 작업을 몇 번 수행하는지 n 에 관련된 식으로 표현해봅니다.

말이 어렵지만 실제로는 그리 어렵지 않습니다. 첫번째 compareToMax 를 생각해봅시다. 임의의 값을 최대값으로 먼저 설정해놓고 배열을 for 문으로 돌면서 최대값 여부를 체크하고 있습니다. for 문을 배열의 크기인 n 번 수행하므로 이런 상황을 O(n) 이라고 표현하고, 선형 시간 내에 수행된다고 합니다. 입력 크기 n 이 증가하는 경우 알고리즘 수행 시간도 선형적으로 비례해 증가하게 됩니다.

여기서 n 에 관한 식을 만들 때 for 문으로 최대값을 확인하는 부분 외에 변수를 초기화하는 부분까지 생각해볼 수 있습니다. 하지만 최고차항의 n 만 고려합니다. 왜냐하면 O(n + 2) 나 O(n) 모두 n 이 매우 커질 경우에는 차이를 무시할 수준이 되기 때문입니다. O(n^2) 과 O(n^2 + n) 도 마찬가지입니다. 즉, 최고차항을 제외한 다른 항은 모두 무시하면 됩니다.

예제에서는 compareToMax 는 n 번 수행되기 때문에 O(n) 이고, compareToAll 은 n 번 작업이 n 번 반복되므로 O(n^2) 이 됩니다. 배열이 커지게 되면 어떻게 될까요? 배열이 커진다는 뜻은 입력값 n 이 커진다는 의미이므로, 5만 건의 데이터가 있으면 compareToMax 은 5만번 수행되지만 compareToAll 은 5만 * 5만 번 수행되므로 입력값이 커질수록 알고리즘 시간이 굉장히 커진다는 것을 알 수 있습니다.

최선, 평균, 최악 케이스

앞서 살펴본 것은 최악의 케이스인 경우입니다. 실행시간이 최대인 케이스에 대해 계산해 본 경우입니다. 만약, compareToAll 알고리즘에서 최대값이 배열의 맨 앞에 있는 경우라면 어떨까요? 그런 경우라면 각 항목에 대해 한번씩만 비교하기 때문에 이 최선의 케이스에서는 O(n) 이 됩니다. 만약 최대값이 배열 가운데에 있는 경우에는 n * (n / 2) 번 수행하기 때문에 O(n^2/2) 이지만 여기서 상수 인자들은 고려하지 않기 때문에 그냥 O(n^2) 으로 봅니다.

compareToMax 의 경우 최대값이 어디에 있던 항상 O(n) 의 실행시간을 갖습니다. 이처럼 어떤 케이스에 초점을 맞추고 생각할 것인지도 고려할 사항입니다.

빅 오 분석법을 적용하는 방법

일반적으로 빅 오 분석법을 적용하는 방법은 다음과 같습니다.

  1. 어떤 값을 n 으로 놓을 것인지 정한다.
  2. 수행해야 할 연산의 횟수를 n 의 식으로 표현한다.
  3. 차수가 제일 높은 항 (최고차항)만 남기고, 모든 상수 인수도 없앤다.

알고리즘 종류 (성능 순)

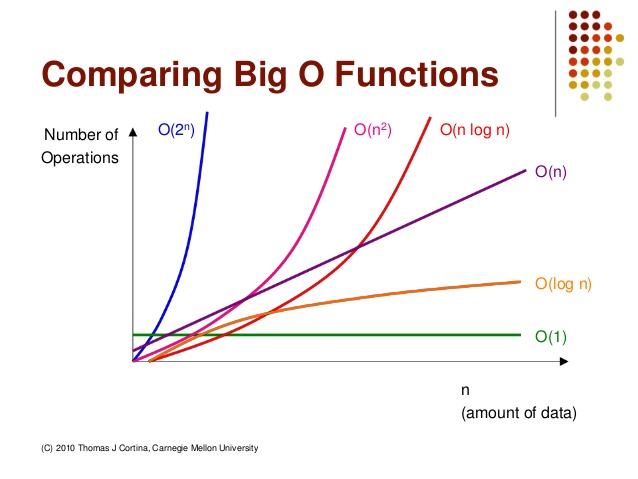
알고리즘 성능 별 그래프

O(1) : 상수 실행 시간 (Constant running time)

입력값과 상관없이 일정한 실행시간을 갖습니다. 가장 바람직한 알고리즘이라고 볼 수 있겠지만 상수 실행 시간 알고리즘이 가능한 경우는 거의 없습니다.

O(log n) : 로그 알고리즘 (Logarithmic algorithm)

실행 시간이 입력 크기의 로그에 비례해서 늘어나는 경우입니다. 그래프를 보시면 아시겠지만 실행시간이 늘어날수록 늘어나는 폭이 줄어들고 있습니다.

O(n) : 선형 알고리즘 (Liniear algorithm)

실행 시간이 입력 크기에 비례하는 알고리즘입니다.

O(n log n) : 초선형 알고리즘 (Superlinear algorithm)

선형 알고리즘 보다는 느리지만 다항식 알고리즘 보다는 빠릅니다.

O(n^c) : 다항식 알고리즘 (Polynomial algorithm)

입력 크기가 늘어나면 실행 시간이 빠르게 늘어납니다.

(c^n) : 지수 알고리즘 (Exponential algorithm)

입력 크기에 따라 실행 시간이 굉장히 빠르게 늘어납니다.

O(n!) : 팩토리얼 알고리즘 (Factorial algorithm)

위 그림에는 나오지 않았지만 가장 느린 알고리즘입니다.

n 이 커지면 실행 시간이 어떻게 변하는지 확인해보겠습니다.

n 10 20
log n 1 1.30
n 10 20
n log n 10 26.02
n^2 100 400
2^n 1,024 1,048,576
n! 3,628,800 2.43 * 10^18

메모리 용량 분석 (Memory footprint)

알고리즘의 메모리 용량이 실행 시간 못지않게 중요한 경우도 있습니다. 이런 경우에는 필요한 메모리 용량을 입력 크기 n 의 식으로 표현해서 따져볼 수 있습니다.

정리

빅 오 분석법을 이용하면 알고리즘의 문제를 풀 때 풀고나서 알고리즘의 성능을 간단하게 예측해볼 수 있습니다. 프로그래밍 면접 시 알고리즘 문제를 풀 때도 면접관이 제시한 풀이에 대해 성능을 물어본 경우에도 빅 오 분석법을 이용해 대답할 수 있습니다. 그리고 알고리즘은 초선형 시간 이상의 성능을 갖는 알고리즘을 사용하는 것이 좋습니다.

Share